В прямоугольном треугольнике ABC катет AC равен 12 см , катет CB равен 9 см. Из вершины...

Question

В прямоугольном треугольнике ABC катет AC равен 12 см , катет CB равен 9 см. Из вершины прямого угла радиусом CB отмечена дуга , отсекающая от гипотенузы отрезок BD . Найдите длину BD

Comments

2 * 9 * 0,6 = 10,8

Answer 1

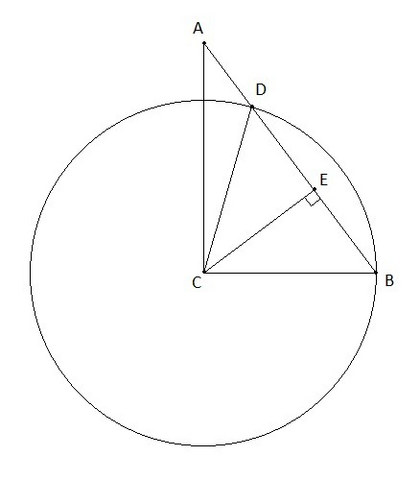
CB =CD = r; ⟹ △BCD – равнобедренный; ⟹ CE – высота, биссектриса, медиана △BCD; ⟹ ∠BCE = 1/2∠BCD.

CE – высота △ABC; ⟹ ∠BCE = ∠A.

По Пифагору:

AB = √(AC² + BC²) = √(12² + 9²) = √225 = 15;

sin∠A = BC/AB = 9 : 15 = 0,6;

BD = 2r * sin(∠BCD/2) = 2 * 9 * 0,6 = 10,8 см.

---