Заданная фигура - сумма двух фигур.
Находим их границы:
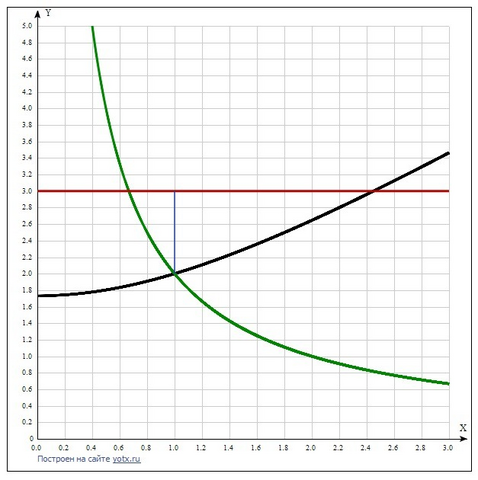
у²-x²=3,
xy=2, у = 2/х, у² = 4/х²: подставим в первое уравнение:
(4/х²) - х² = 3,
(х⁴ + 3х² - 4 )/х² = 0.
Если х не равен
нулю, то можно приравнять нулю только числитель:
(х⁴ + 3х² - 4) = 0.
Решаем это
уравнение и его корни будут точками пересечения с Ох:
Замена: х² = а.
Тогда получим квадратное уравнение:
а² + 3а - 4 = 0.
Квадратное уравнение, решаем относительно a: Ищем дискриминант:
D=3^2-4*1*(-4)=9-4*(-4)=9-(-4*4)=9-(-16)=9+16=25;Дискриминант больше 0, уравнение имеет 2 корня:
a_1=(√25-3)/(2*1)=(5-3)/2=2/2=1; a_2=(-√25-3)/(2*1)=(-5-3)/2=-8/2=-4.
Этот корень не принимаем (х² ≠ -4).
Получаем х = √а и 2 значения: х = 1 и х = -1 (это значение не принимаем - не соответствует общей области определения).
Значение у = 2/1 = 2.
Объём равен интегралу функций относительно квадрата х.

.

.
Плоская фигура приведена в приложении.