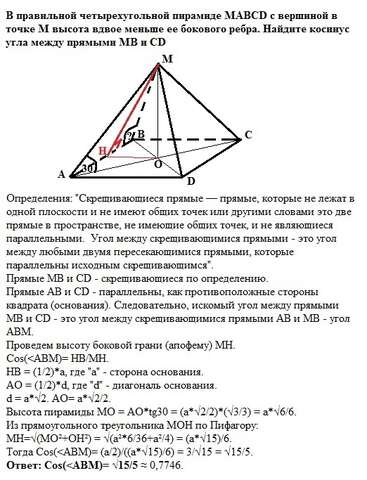
Определения: "Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости и не имеют общих точек или другими словами это две прямые в пространстве, не имеющие общих точек, и не являющиеся параллельными. Угол между скрещивающимися прямыми - это угол между любыми двумя пересекающимися прямыми, которые параллельны исходным скрещивающимся".
Прямые МВ и CD - скрещивающиеся по определению.
Прямые АВ и CD - параллельны, как противоположные стороны квадрата (основания). Следовательно, искомый угол между прямыми МВ и CD - это угол между скрещивающимися прямыми АВ и МВ -
угол ABM.
Проведем высоту боковой грани (апофему) МН.
Cos(НВ = (1/2)*а, где "а" - сторона основания.
АО = (1/2)*d, где "d" - диагональ основания.
d = a*√2. AO= a*√2/2.
Высота пирамиды MO = АО*tg30 = (a*√2/2)*(√3/3) = a*√6/6.
Из прямоугольного треугольника МОН по Пифагору:
МН=√(МО²+ОН²) = √(а²*6/36+а²/4) = (а*√15)/6.
Тогда Cos(Ответ: Cos( ≈ 0,7746.