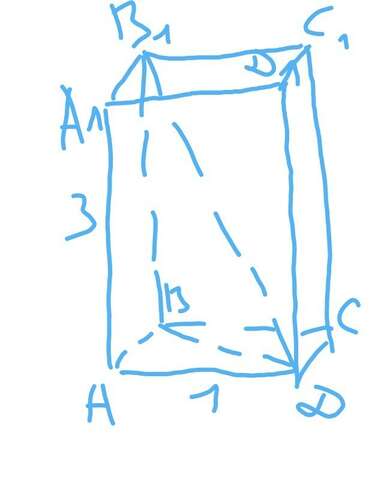
1. По теореме Пифагора из треугольника BB1D:
B1D^2 = BB1^2 + BD^2
BD^2 = B1D^2 - BB1^2 = 5^2 - 3^2 = 25 - 9 = 16
BD = 4.
По теореме Пифагора из треугольника ABD:
AB^2 + AD^2 = BD^2
AB^2 = BD^2 - AD^2 = 16 - 1 = 15
AB = sqrt(15).
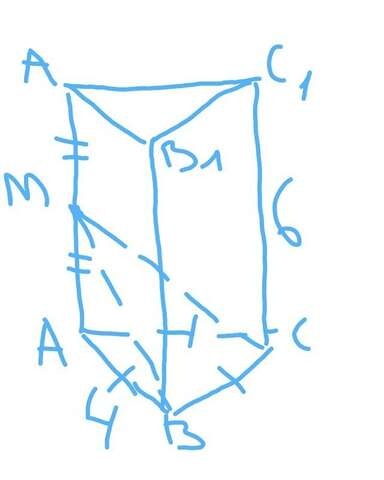
2. Искомое сечение - треугольник BMC.
По теореме Пифагора из треугольника ABM:
BM^2 = AM^2 + AB^2
AM = 1/2 AA1 = 1/2 * 6 = 3 (см)
BM^2 = 9 + 16 = 25
BM = 5 (см).
Т.к. AC=AB, то очевидно, что BM=CM.
Проведем высоту в треугольнике BMC. Т.к. треугольник равнобедренный (BM=CM), то высота MH является так же медианой. То есть BH= CH = 1/2 BC = 1/2 * 4 = 2 (см).
Исходя из теоремы Пифагора, MH^2 = BM^2 - BH^2 = 25 - 4 = 21, MH= sqrt (21)
S = 1/2 * MH * BC = 1/2 * 4 * sqrt (21) = 2sqrt (21).
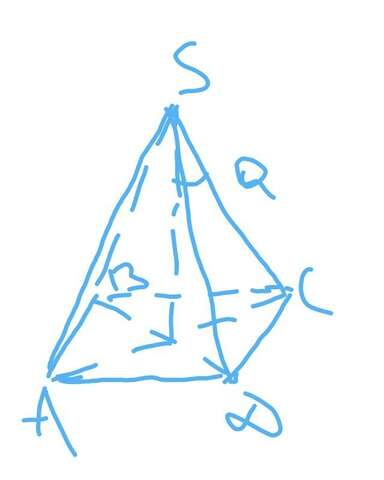
3. Рассмотрим треугольник SOC, где O - это основание высоты пирамиды (точка пересечения диагоналей).
Угол OSC = 45, SC= a. Т.к. SO - высота, то угол SOC = 90, угол SCO = 180-90-45 = 45.
Значит, SO=OC.
SO^2 + OC^2 = SC^2
2SO^2 = SC^2
2SO^2 = a^2
SO^2 = a^2/2,
SO = a/sqrt (2) = OC
AC = 2*OC = 2a/sqrt (2) = a*sqrt (2)
Так как пирамида правильная, то в основании лежит квадрат.
Значит, AD^2+CD^2 = AC^2 = 2a^2
2AD^2 = 2a^2
AD^2 = a^2
AD=a.