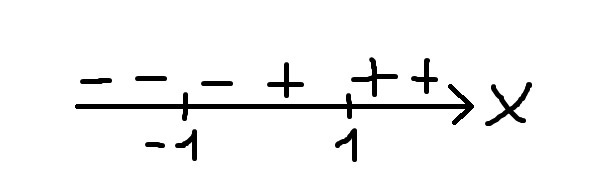По методу интервалов (1):
x - 1: - - +
x + 1: - + +
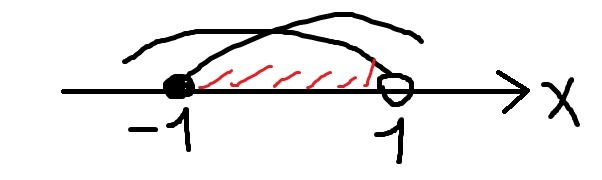
1 случай:


 -2 \\ \end{cases} \end{equation*} " alt=" \begin{equation*} \begin{cases} x<-1 \\ x > -2 \\ \end{cases} \end{equation*} " align="absmiddle" class="latex-formula"> (2)
-2 \\ \end{cases} \end{equation*} " alt=" \begin{equation*} \begin{cases} x<-1 \\ x > -2 \\ \end{cases} \end{equation*} " align="absmiddle" class="latex-formula"> (2)

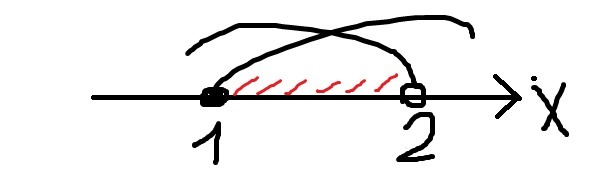
2 случай:

 (3)
(3)

3 случай:

 (4)
(4)
Объединим множество решений:

Ответ: x∈(-2;2)