Кто знает как решить????

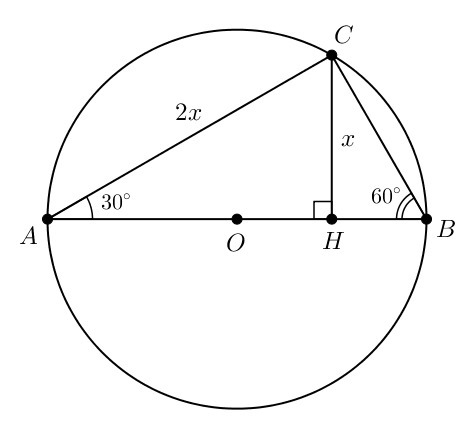
Обозначим CH как x, а AC — как 2x (см. рисунок). Очевидно, Δ ACH — прямоугольный треугольник, AC — гипотенуза. Сначала найдём угол A по теореме синусов:

$\displaystyle \frac{2x}{\sin 90^{\circ}}=\frac{x}{\sin \angle A}}\\ \frac{1}{\sin \angle A}=2 \\ \sin \angle A= \frac{1}{2}; \\ \angle A= 30^{\circ}$

(При условии, что 0°<∠A<90°, поэтому значение ∠A=150° не подходит.)<br>

Кстати, угол можно вычислить быстрее, если вспомнить, что когда катет в два раза меньше гипотенузы, то противолежащий к нему угол равен 30°.

Угол ∠ACB равен 90°, поскольку опирается на диаметр окружности. Поэтому ∠ABC = 180°–(90°+30°)=180°–120°=60°.