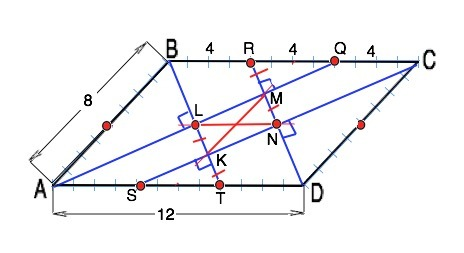
Дан параллелограмм ABCD с длинами сторон 12 и 8. Биссектрисы его углов при пересечении образуют четырехугольник. Чему равна длина диагоналей этого четырехугольника?
-----------------
По свойству параллельных прямых и секущей сумма углов при одной стороне параллелограмма равна 180°. Следовательно, биссектрисы его соседних углов пересекаются под прямым углом. Поэтому четырехугольник, образованный четырьмя биссектрисами параллелограмма - прямоугольник.
Обозначим его вершины К, L, M и N.
Биссектрисы параллелограмма, являясь секущими, отсекают от него равнобедренные треугольники ( они делят углы пополам, и накрестлежащие углы тоже равны). Противоположные стороны параллелограмма равны =>
АВ=BQ=AT=CD=CR=DS=8 Тогда
ВR=12-CR=4. Аналогично длина отрезков QC,, DT,, AS равна 4.
Отрезки QR и TS равны 12-2•4=4.
По первому признаку равенства треугольников
∆ АВТ=∆ RCD и ∆ ABQ=∆ ADC - их стороны и углы, заключённые между ними, равны.
В равнобедренном треугольнике биссектриса=высота=медиана.
BL=LT=RN=ND
Биссектрисы противоположных углов параллелограмма параллельны ВТ║RD, BR║TD как лежащие на параллельных сторонах ABCD..
Из равенства ∆ АBL и ∆ CBD следует BL=RN. =>
Четырехугольник BRNK- параллелограмм, ⇒LN=BR=4
LN - диагональ прямоугольника KLMN. Диагонали прямоугольника равны.
КМ=LN=4 (ед. длины)