Стороны треугольника равны 55, 55, 66 см. Найти площадь треугольника, вершинами которого...

Question

Стороны треугольника равны 55, 55, 66 см. Найти площадь треугольника, вершинами которого служат основания биссектрис данного треугольника.

Comments

h=√(55^2-(66/2)^2)=44; S=44*66/2=1452

---

неверно...

---

30*24/2=360

---

Площадь не того треугольника я посчитал))) h/33=tg(a/2)=sin(a)/(1+cos(a))=(44/55)/(1+33/55)=(4/5)/(8/5)=1/2; h=33/2=16,5; Пусть основание будет x, тогда (44-16,5)/x=44/66; x=66*27,5/44=41,25. S=41,25*16,5/2=340,3125

---

опять не то...все проще и точнее

Answer 1

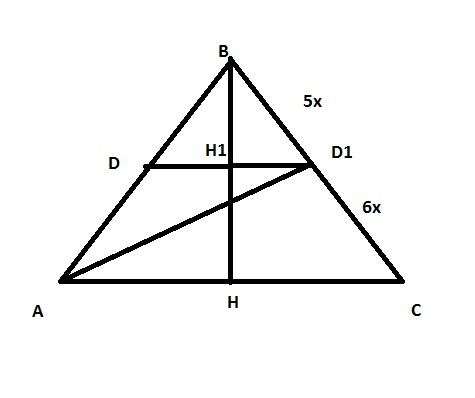
Надо найти S ΔDD1H=DD1*HH1/2

Биссектриса делит противоположную сторону пропорционально прилежащим сторонам в треугольнике

AD1 делит ВС на BD1= 5х и D1C=6х

5х+6х=11х=55; x=5; BD1=25; D1C=30

треугольники НВС и Н1ВD1 подобны по 2 углам с k=11/5

H1D1=HC/k=33/(11/5)=15

HD=2H1D1=30

BH^2=BC^2-HC^2=55^2-33^2=44^2; BH=44

HH1=HB-BH1=44-HB/(11/5)=44-44/(11/5)=44-20=24

S=30*24/2=360

---