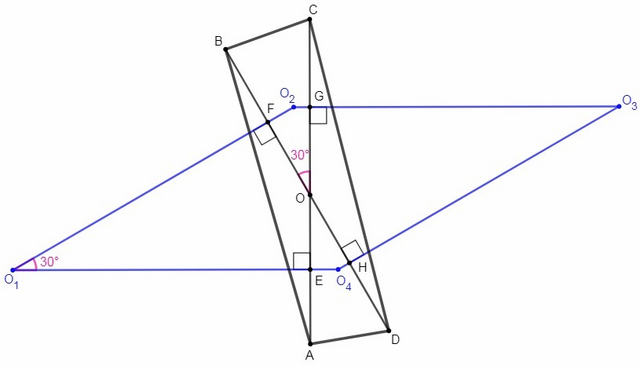
Центром описанной окружности является точка пересечения серединных перпендикуляров к сторонам, в данном случае - к отрезкам диагоналей. Перпендикуляры, проведенные к одной диагонали, параллельны - O₁O₂||O₃O₄, O₁O₄||O₂O₃. Противоположные стороны параллельны, O₁O₂O₃O₄ является параллелограммом.
S(ABCD)= AC*BD*sin30 /2 <=> AC*BD = 6*4 =24
E, F, G, H - середины AO, BO, CO, DO
В четырехугольнике O₁FOE противоположные углы прямые, следовательно сумма другой пары противоположных углов так же равна 180.
∠FO₁E +∠FOE =180
∠FOG +∠FOE =180
∠FO₁E=∠FOG =30
O₂K - высота на O₁O₄. Катет, лежащий против угла 30, равен половине гипотенузы.
O₂K= O₁O₂/2
O₂K= GE =AC/2 => O₁O₂=AC
FH=BD/2
S(O₁O₂O₃O₄)= O₁O₂*FH = AC*BD/2 =24/2 =12