Помогите с векторами! (Вложение)

0 голосов
29 просмотров

Помогите с векторами! (Вложение)

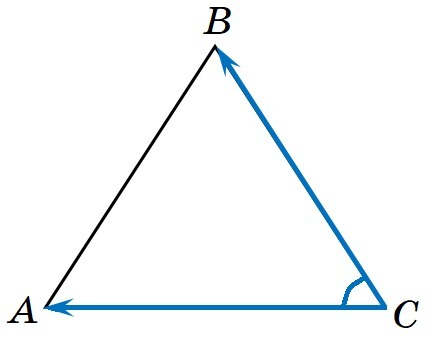
image
Геометрия (1.2k баллов) | 29 просмотров
0

ответ №3

оставил комментарий (830k баллов)
Дано ответов: 2
0 голосов
Правильный ответ

Достроим равносторонний треугольник до параллелограмма.

По правилу параллелограмма сложения векторов имеем:


\overline {CA}+\overline {CB}=\overline {CD}\\\\|\overline {CA}|=|\overline {CB}|=|\overline {AB}|=a\; \; \Rightarrow \; \; AO=BO\; ,\; \; AO\perp AB\; \; \Rightarrow \\\\|\overline {CO}|=\sqrt{a^2-(\frac{a}{2})^2}=\frac{a\sqrt3}{2}\\\\|\overline {CD}|=2\cdot |\overline {CO}|=2\cdot \frac{a\sqrt3}{2}=a\sqrt3

(830k баллов)
0

Спасибо!

оставил комментарий (1.2k баллов)
0 голосов

Дано: ΔАВС - равносторонний |СА| = a, |CB| = a, ∠(CA, CB) = 60°.

Найти: |CA + CB| - ?

Решение. Существует такое равенство: |х|² = х². Оно поможет нам найти значение |CA + CB|. Итак, воспользуемся формулой: (CA + CB)² = СА² + 2СА×СВ + СВ² = а² + 2 × а × а × сos60° + a² = a² + а² + а² = 3а² ⇒ |CA + CB| = √3а² = а√3.

Ответ: а√3.

Замечание: CA, СВ и х расписаны в векторном виде.

image
(4.2k баллов)
0

2СА×СВ - это скалярное произведение векторов, поэтому оно равно а × а × сos∠(CA, CB)°

оставил комментарий (4.2k баллов)
0

2×СА×СВ - это скалярное произведение векторов, поэтому оно равно 2 × а × а × сos∠(CA, CB)

оставил комментарий (4.2k баллов)
0

Спасибо!

оставил комментарий (1.2k баллов)
Похожие задачи