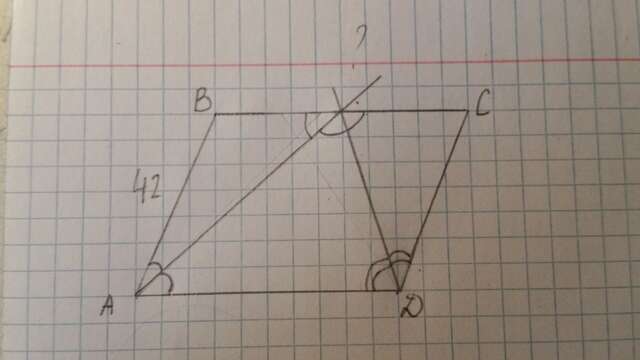
Пусть точка K - точка пересечения бисектрисс на стороне BC.
1. т.к ABCD - параллелограмм, AB║CD, BC║AD ;
∠CKA=∠BAK, ∠BKA=∠KAD ( как внутренне-накрест лежащие при BC║AD и сек. AK
т.к AK- , бисектрисса, ∠BAK=∠KAD, значит∠CKA=∠BAK=∠BKA=∠KAD ⇒ Δ ABK - р/б. ⇒ AB=BK=42.
2. т.к. Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник , KC =CD= 42 (т.к. AB=Bc т.к. параллелограмм).
3. BC=BK+KC=42+42=84
Ответ: 84 см