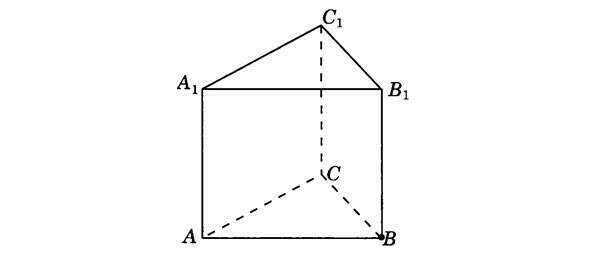
1) Все боковые ребра правильной треугольной призмы перпендикулярны основаниям.
Так как А1М1 лежит в плоскости А1В1С1, то АА1 перпендикулярно А1М1
Значит, ∆ АА1М1 - прямоугольный
2) Рассмотрим ∆ А1В1С1 ( А1В1 = В1С1 = А1С1 ) :
В равностороннем треугольнике высота равна h = a√3/2
A1M1 = 4√3 × √3/ 2 = 6
AA1 = 2√7
3) Рассмотрим ∆ АА1М1 ( угол АМ1А1 = 90° ):
По т. Пифагора:
АМ1² = АА1² + А1М1²
АМ1² = ( 2√7 )² + 6² = 28 + 36 = 64
АМ1 = 8
сos угол АМ1А1 = А1М1/ АМ1 = 6/8 = 3/4 = 0,75
ОТВЕТ: 0,75