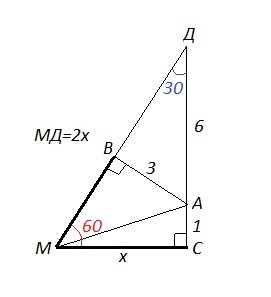
Так как точка А расположена внутри угла в 60° (∠М=60°) и удалена от его сторон на расстояние 3 см и 1 см, то длина перпендикуляра, проведённого от точки А до стороны МВ равно 3 см (АВ⊥МВ, АВ=3 см),
а длина перпендикуляра, проведённого от точки А до стороны МС, равна 1 см (АС⊥МС , АС=1 см).
Получили два прямоугольных треугольника: ΔАВМ и ΔАСМ,
∠АВМ=90° , ∠АСМ=90° .
Продлим сторону АС до пересечения со стороной МВ в точке Д. Получим ΔДМС, в котором ∠ДМС=60°, ∠ДСМ=90° .
В прямоугольном ΔДМС острые углы будут ∠ДМС=60° и
∠СДМ=90°-60°=30° .
Против угла в 30° в прямоугольном треугольнике лежит катет, равный половине гипотенузы, то есть СМ=0,5*МД ⇒ МД=2*СМ .
Для более удобной записи обозначим СМ=х, тогда МД=2х.
Рассм. ещё один прямоугольный треугольник, в котором один из острых углов равен 30°. Это ΔАВД. ∠АВД=90 , ∠АДВ=30°.
Катет АВ лежит против угла в 30° ⇒ АД=2*АВ ⇒ АД=2*3=6.
Катет СД прямоугольного ΔДМС равен СД=СА+АД=1+6=7 см,
а по теореме Пифагора МД²=СД²+МС² ⇒ (2х)²=7²+х² ⇒
4х²=49+х² , 3х²=49 , х²=49/3 , х=7/√3 .
МС=7/√3 .
Из ΔАМС: АМ²=СМ²+АС² ⇒ АМ²=1²+(7/√3)² , АМ²=1+49/3=52/3 ,
АМ=√(52/3)≈√(17,33)≈4,16
или АМ=√52/√3=√(4·13)/√3=(2·√13)/√3=(2√39)/3 .