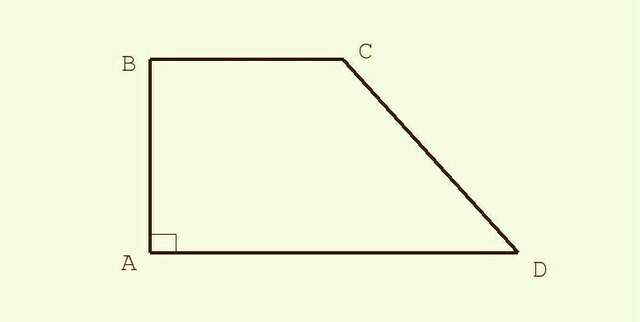
1) Опустим из точки С на AD высоту СН , тогда
S abcd = 1/2 × ( BC + AD ) × СН
220 = 1/2 ( 10 + 34 ) × CH
220 = 22 × CH
CH = АВ = 10 cm
BC = AH = 10 cm
HD = 34 - 10 = 24 cm
2) Рассмотрим ∆ CDH ( угол CHD = 90° ):
По теореме Пифагора:
CD² = CH² + HD²
CD² = 10² + 24² = 100 + 576 = 676
CD = 26 см
Боковые ребра прямоугольной трапеции равны:
АВ = 10 см
CD = 26 cм
Большая боковая сторона AD, которая равна 26 см
ОТВЕТ: 26