1) В равнобедренном треугольнике высота, проведённая к боковой, делит эту сторону **...

Question 1

1) В равнобедренном треугольнике высота, проведённая к боковой, делит эту сторону на отрезки длинной 12 см и 3 см, считая от вершины треугольника, противолежащей основанию. Найдите площадь и периметр треугольника.

Question 2

Дано:

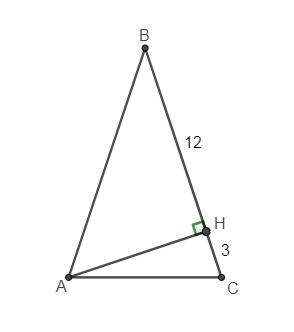
ΔАВС

АВ = ВС

АН - высота

ВН = 12 см

СН = 3 см

Найти: Р(АВС); S(ABC)

Треугольник АВС равнобедренный ⇒ АВ = ВС = 12 + 3 = 15 см

Из ΔАВН по теореме Пифагора:

$AH = \sqrt{AB^2-BH^2}=\sqrt{15^2-12^2} = \sqrt{225-144} = \sqrt{81} = 9$ см

Из ΔАСН по теореме Пифагора:

$AC = \sqrt{AH^2+CH^2}=\sqrt{9^2+3^2} = \sqrt{81+9} = \sqrt{90} = 3\sqrt{10}$ cм

Периметр треугольника равен сумме трёх сторон:

$P_{ABC}=AB+BC+AC=15+15+3\sqrt{10}=30+3\sqrt{10}$ cм

Площадь треугольника равна половине произведения основания на высоту:

$S_{ABC}=\frac{1}{2}\cdot BC \cdot AH = \frac{1}{2}\cdot 15 \cdot 9 =67.5$ cм ²

Banabanana_zn · Answer 1 · 2018-09-10T18:46:11+0000