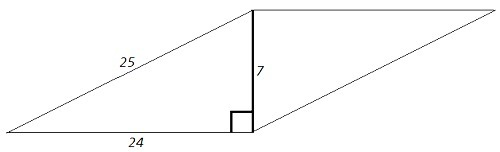
25^2 -24^2 =(24-25)(24+25) =49 =7^2 => 7^2 +24^2 =25^2
Треугольник со сторонами 7, 24, 25 - прямоугольный (для длин выполняется теорема Пифагора), 7 и 24 - длины катетов.
Расстояние между параллельными прямыми - длина перпендикуляра, опущенного из точки одной прямой на другую прямую. Противоположные стороны параллелограмма равны и параллельны. Диагональ длиной 7 перпендикулярна меньшей стороне параллелограмма и является искомым расстоянием.
Ответ: 7