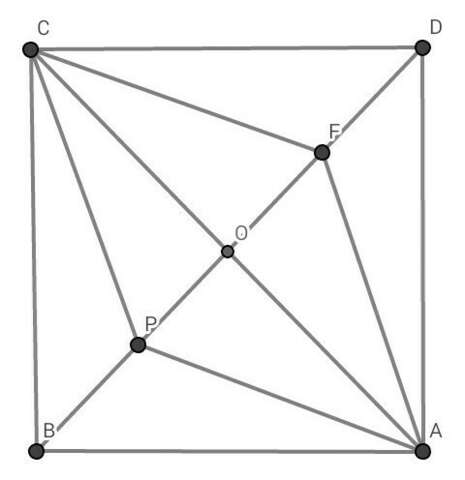
ДАНО: АВСD - квадрат ; P € BD ; F € BD ; APK = 60° ; PF = 6 см
НАЙТИ: Р apcf
_________________________
РЕШЕНИЕ:
Точка К - это перечение прямых СР и АВ.
Перед тем, как искать периметр четырёхугольника АРСF, необходимо раскрыть его вид , основываясь на признаки четырёхугольников:
1) ∆ CBP = ∆ АВР = ∆ АDF = ∆ CDF по двум сторонам и углу между ними:
АВ = ВС = CD = AD - по свойству квадрата
ВР - общая сторона у ∆ СВР и ∆ АВР
FD - общая сторона у ∆ CDF и ∆ АDF
К тому же BP = FD - по условию
угол CBP = угол АВР = угол CDF = угол ADF - по свойству диагоналей квадрата
2) В равных треугольниках соответственно равные стороны:
АР = РС = СF = АF
AC перпендикулярен ВD
CO = OА = ВО = ОD - по свойству пересечения диагоналей квадрата
Но ВР = FD и ВО = OD =>
Значит, РО = ОF
Следовательно, у данного четырёхугольника APCF все стороны равны ( этого было бы достаточно, чтобы найти его периметр ) , диагонали взаимно перпендикулярны и точкой пересечения делятся пополам. И к тому же внешний угол равен 60°, это доказывает, что четырёхугольник АРСF не квадрат.
Поэтому, четырёхугольник АРСF является ромбом.
3) угол АРС = 180° - угол АРК = 180° - 60° = 120°
угол СРF = угол APF = 1/2 × угол АРС = 1/2 × 120° = 60° - по свойству диагоналей ромба. Диагонали ромба являются биссектриса его углов.
4) Рассмотрим ∆ СPF:
∆ CPF - равнобедренный, СР = CF
Углы при основании равнобедренного треугольника равны:
угол CPF = угол CFP = 60°
угол PCF = 180 ° - 60° - 60° = 60°
Значит, ∆ CPF - равносторонний =>
PC = PF = CF = 6 см
Р apcf = AP + PC + CF + AF = 4 × PC = 4 × 6 = 24 см
ОТВЕТ: 24 см.