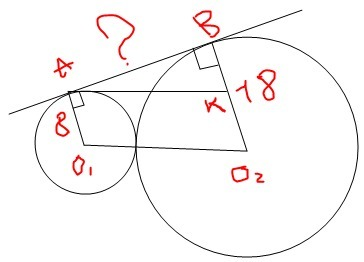
АВ - дотична, О₁А = 8 см і О₂В = 18 см - радіуси кіл, О₁О₂ = 8 + 18 = 26 см - відстань між центрами кіл
Оскільки радіуси кіл перпендикулярні до дотичної, то О₁А||О₂В, тому чотирикутник О₁АВО₂ - прямокутна трапеція з основами О₁А і О₂В.
Проведемо відрізок АК||О₁О₂, тоді О₁АКО₂ - паралелограм (О₁А=КО₂ = 8 см; АК = О₁О₂ = 26 см). З ΔАКВ (∠В = 90°): АВ = √(АК² - КВ²), де КВ = О₂В - О₂К = 18 - 8 = 10 см. Отже, АВ = √(26² - 10²) = АВ = √(16 · 36) = 4 · 6 = 24 см.
Відповідь: 24 см.