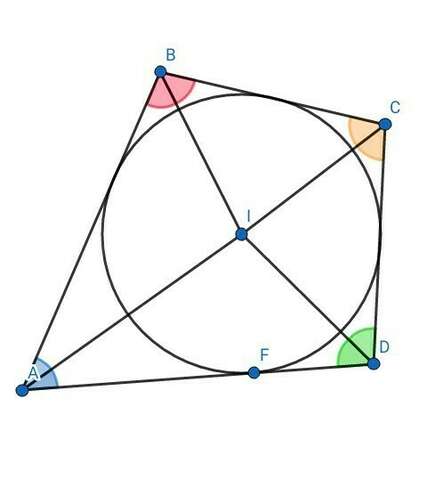
ДАНО: АВСD - четырёхугольник ; вписанная окружность ( I ; r ) ; угол А = 47° ; угол С = 99°
НАЙТИ: угол АIB + угол CID
________________________
РЕШЕНИЕ:
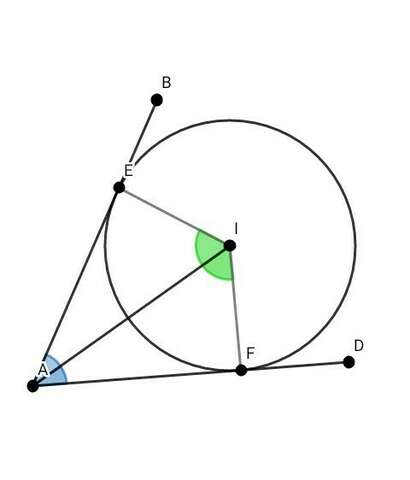
1) ( см. рис. 2 ) По признаку равенства прямоугольных треугольниках :
∆ АIF = ∆ АIE - по катету и гипотенузе ( ЕI = FI - как радиусы окружности ; AI - общая сторона )
В равных треугольниках соответственно равные элементы ( стороны и углы ) =>
угол ЕАI = угол IAF = 47°/ 2 = 23,5°
2) ( см. рис. 1 ) Аналогично, угол ABI = угол CBI ; угол BCI = угол DCI = 99°/ 2 = 49,5° ,
угол ADI = угол CDI
Пусть угол ABI = а , угол CDI = b, тогда
Сумма углов в любом выпуклом четырёхугольник равна 360°

3) Рассм. ∆ АВI:
Сумма всех углов в любом треугольнике всегда равна 180° :
угол АIB = 180° - 23,5 - a
Соответственно, угол CID = 180° - 49,5 - b
Значит, угол AIB + угол CID =

________________________
P.S. Можно было обойтись без данных углов
1) Пусть угол ВАI = a , угол ABI = b , угол DCI = c , угол CDI = d
Сумма углов в любом выпуклом четырёхугольник равна 360°
2a + 2b + 2c + 2d = 360°
a + b + c + d = 180°
2) Рассм. ∆ АВI:
Сумма всех углов в любом треугольнике всегда равна 180° :
угол АIB = 180° - a - b
Соответственно, угол CID = 180° - c - d
Значит, угол AIB + угол CID = 180° - a - b + 180° - c - d = 360° - ( a + b + c + d ) = 360° - 180° = 180°
ОТВЕТ: угол AIB + угол CID = 180°