Основание пирамиды является прямоугольник со сторонами 10 см и 24 см боковые ребра...

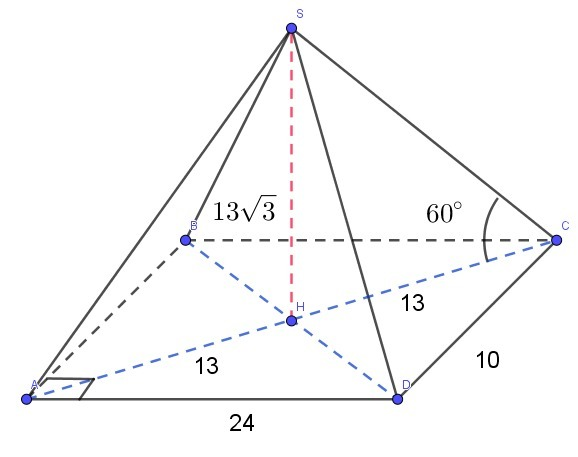
Если в основании - прямоугольник и все ребра наклонены к основанию под одним и тем же углом, то высота пирамиды падает в точку пересечения диагоналей прямоугольника.

SH - высота

Диагональ АС найдем по теореме Пифагора:

$AC=\sqrt{AD^2+CD^2}=\sqrt{24^2+10^2} =26$

Диагонали прямоугольника точкой пересечения делятся пополам

$HC=\frac{AC}{2} =\frac{26}{2} =13$

$SH=13*tg60^\circ =13\sqrt{3} \\ \\ V=\frac{1}{3} S_oh=\frac{1}{3} *24*10*13\sqrt{3}= 1040\sqrt{3}$

Ответ: 1040√3 см³