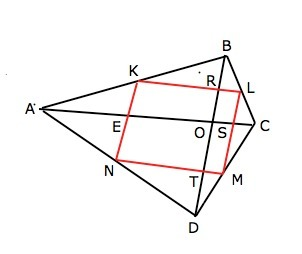
Проведем в данном четырехугольнике диагонали АС и BD. Точку пересечения обозначим О. Точку пересечения KN и АС обозначим Е, LM и АС – S, KL и BD – R, MN и BD – T.
Пусть площадь треугольника АВО=а, АDO=b, BCO=e, DCO=f
Стороны четырехугольника KLMN параллельны диагоналям исходного и являются средними линиями треугольников. на которые диагонали его делят. ∆ АКЕ=∆ KBR. По свойству площадей подобных фигур площадь каждого равна 1/4 площади ∆ АВО, т.е. a/4, и тогда площадь КROE=а- a/4-a/4=a/2. Аналогично площадь RLSO=e/2; площадь SMTO=f/2 и площадь NEOT=b/2. По условию площадь АВСD=24 и равна сумме треугольников. на которые диагонали делят его.
Тогда а+b+e+f=24. Площадь КLMN=a/2+b/2+e/2+f/2=(a+b+e+f):2=24:2=12 см²