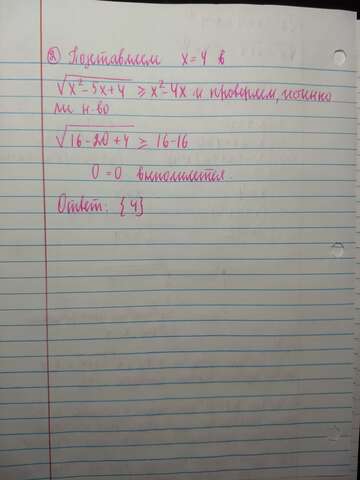Такое очень tricky неравенство :)
Я умышленно переписал систему так, чтобы нижнее неравенство являлось первым. С него и начнём. Аккуратно возведя в квадрат обе части данного неравенства, указав дополнительные условия равносильно но преобразования, мы получаем систему из трёх простых неравенство. Решением будет являться единственная точка x=4.
Затем, нам осталось подставить данную точку во второе "страшное" неравенство исходной системы (страшное, потому что при возведении в квадрат обоих частей, даже после упрощения, мы получим (x-4)(x^3-4x^2-x+1)=<0). <br>Итак, подставляем x=4 во второе неравенство исходной системы (корень равен x^2-4x), убеждаемся, что неравенство истинно и превращается в тождество 0=0.
Ответ: x=4
На фото решение. Удачи вам!