Объясните пожалуйста как отбираются корни, почему не от 0 до pi, а от pi/6. от корня до...

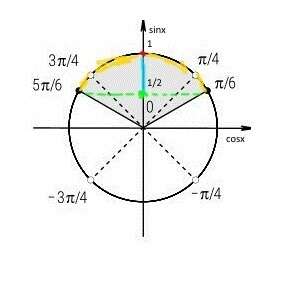
На оси sinx отмечаем точки 1/2 (на рисунке - зеленым цветом) и 1 (на рисунке - красным цветом). Так как нам нужно 1/2≤sinx≤1, то нас интересует отрезок между красной и зеленой точками (на рисунке - голубым цветом). Проецируем голубой отрезок на единичную окружность и получаем дугу (на рисунке - желтым цветом), которая и является интервалом решений. Найдем названия точек, являющихся концами дуги. Для этого решим уравнение:

$\bf sinx=\dfrac{1}{2} \ \Rightarrow \ x= \left[\begin{array}{I} \dfrac{\pi}{6}+ 2\pi k \\ \dfrac{5 \pi }{6 }+ 2 \pi k \end{array}}$

Значит решениями являются [п/6+2пk; 5п/6+2пk].

Осталось лишь выколоть x=п/4+пn/2 и получится ответ.