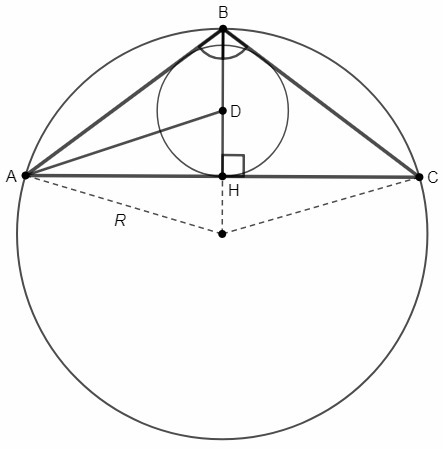
AC=8
BH - высота к основанию AC.
D - центр вписанной окружности △ABC.
BD/DH =5/4
Высота в равнобедренном треугольнике является биссектрисой и медианой.
∠ABH=∠ABC/2
AH=AC/2 =8/2 =4
Центром вписанной окружности треугольника является точка пересечения биссектрис.
AD - биссектриса в △ABH.
По теореме о биссектрисе
AB/AH=BD/DH =5/4 <=> AB=5
△ABH - египетский треугольник (3:4:5), BH=3
sin(ABH)=AH/AB =4/5
cos(ABH)=BH/AB =3/5
sin(ABC)= sin(2ABH) =2sin(ABH)cos(ABH) = 2 *4/5 *3/5 =24/25
По теореме синусов
AC/sin(ABC) =2R <=> R= 4 *25/24 =25/6