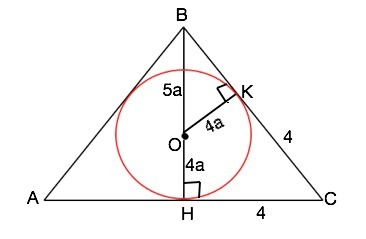
Центр окружности, вписанной в равнобедренный треугольник с основанием, равным 8, делит высоту. проведенную к основанию, в отношении 5:4, считая от вершины треугольника. Найти радиус описанной окружности.
Обозначим треугольник АВС, АВ=ВС, АС=8. О- центр вписанной окружности, ВН - высота ( и медиана, т.к. ∆АВС равнобедренный). ВО:ОН=5:4 Примем коэффициент отношения ВО:ОН равным а. Проведем радиус ОК в точку касания. Прямоугольные треугольники ВНС и ВКО имеют общий угол В, ⇒ они подобны. Из отношения катета и гипотенузы 4:5 треугольник - египетский ⇒ в ∆ ВОК катет ВК=3а. ( то же и по т. Пифагора ) . Из подобия следует отношение ВН:ВК=СН:ОК, т.е. 9а:3а=4:4а, откуда а=1/3. ВК=1. ВН=9•1/3=3. СК=СН (отрезки касательных из одной точки). Тогда ВС=АВ=ВК+КС=5.
По т.синусов2R=AB:sin C ⇒ 2R=АВ:(ВН/ВС) ⇒ R=5:(3/5):2=25/6=4¹/₆ (ед. длины) ------- Тот же ответ получим, если найдем радиус описанной окружности по формуле R=abc/4S