у(х) примет наибольшее значение, когда дробь примет наибольшее значение, а это будет, когда у1(х)=4х²-4х+3 примет наименьшее значение.
Дело в том, что у1(х)>0
Действительно,
функция у1(х) не имеет корней, т.к дискриминант
у1(х) :D=16-4*4*3<0<br>и раз а=4>0,
значит парабола будет вся над осью абсцисс.
то есть 4х²-4х+3>0
найдем производную:
(4х²-4х+3)'=8х-4=0
Х*=½
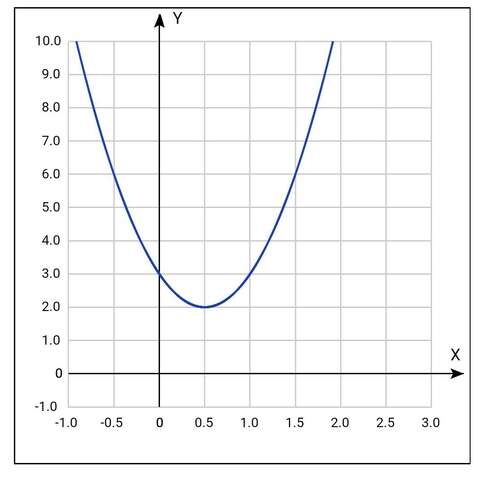
если не проходили производную, то можно построить параболу
у1=4х²-4х+3 (см фото)
её вершина будет в точке
х*= -b/2a=-(-4)/(2*4)=½
и у1(х*)=2
у1 будет иметь минимум,
а наша функция
у(х)=1+( 1/у1(х))
будет иметь максимум и он равен:
f(Х*)=
=1+1/(4(1/2)²-4(1/2)+3)=1+1/(1-2+3)=1½
Ответ у наиб =1,5