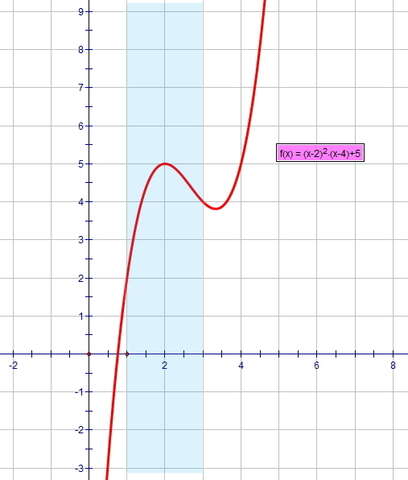
перепишем так:
у = (х²-4х+4) * (х-4) + 5 = х³ - 8х² + 20х - 11 (проще брать производную...)
производная: у⁾ = 3х² - 16х + 20 = 0 (условие для нахождения экстремумов)
D = 16²-12*20 = 16(16-15) = 4²; корни: (16-4)/6 = 2 и (16+4)/6 = 10/3 = 3¹/₃
+++++++(2)----------(3¹/₃)+++++++++ это знаки производной...
там, где (+) функция возрастает, там где (-) функция убывает, т.е. максимум достигается при х=2 (это на указанном отрезке)
у(2) = 0 * (-2) + 5 = 5
можно проверить: у(1) = (-1)² * (-3) + 5 = 2... у(3) = 1² * (-1) + 5 = 4