К телу массой m=1кг, находящемуся ** наклонный плоскости с углом наклона a=30˚, приложена...

Question

Дан 1 ответ

nikbodnarnik_zn · Answer 1 · 2018-09-14T04:02:45+0000

Дано:

$m = 1$ кг

$\alpha = 30^{\circ}$

$F_{_{T}} = 10$ Н

$\mu = 0,2$

$g = 10$ м/с²

========================

Найти: $a - ?$

========================

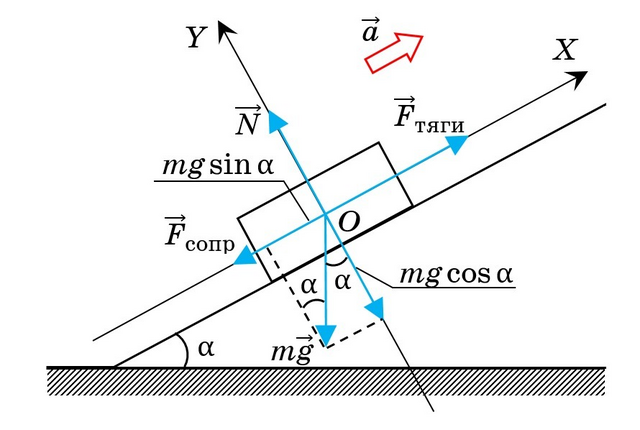
Решение. На тело действуют четыре силы: сила тяжести $m\vec{g}$ , сила $\vec{N}$ нормальной реакции опоры, сила тяги $\vec{F}_{_{T}}$ и сила сопротивления $\vec{F}_{_{CO\varPi P}}$ .

Тело увеличивает свою скорость, поэтому ускорение движения тела направлено в сторону направлению его движения.

Выполним пояснительный рисунок, указав на нём милы, действующие на тело, направления скорости и ускорения движения.

Свяжем систему координат с телом на поверхности Земли, ось OY направим перпендикулярно поверхности, ось OX - вдоль дороги (при таком выборе осей только одна сила ( $m\vec{g}$ ) не лежит на осях координат).

Запишем второй закон Ньютона в векторном виде:

$\vec{F}_{_{T}} + \vec{N} + m\vec{g} + \vec{F}_{_{CO\varPi P}} = m\vec{a}$ .

Спроецируем уравнение на оси координат (сила $m\vec{g}$ не лежит на оси координат, поэтому для нахождения её проекций опустим из конца вектора $m\vec{g}$ перпендикуляры на оси OX и OY: $mg_{x} = -mgsin\alpha; mg_{y} = -mgcos\alpha$ ) и запишем выражение для $F_{_{CO\varPi P}}$ :

$\left \{ {{OX: F_{_{T}} - F_{_{CO\varPi P}} - mgsin\alpha = ma} \atop {OY = N - mgcos\alpha = 0 \ \ \ \ \ \ \ \ \ \ \ \ \ }} \right. \\ F_{_{CO\varPi P}} = \mu N.$

Решив полученную систему уравнений, найдём $a$ :

$N = mgcos\alpha$ ⇒ $F_{_{CO\varPi P}} = \mu mgcos\alpha$ ⇒ $F_{_{T}} - \mu mgcos\alpha - mgsin\alpha = ma$ ⇒ $\boxed {a = \dfrac{F_{_{T}} - mg(\mu cos\alpha - sin\alpha)}{m}}$ - окончательно.