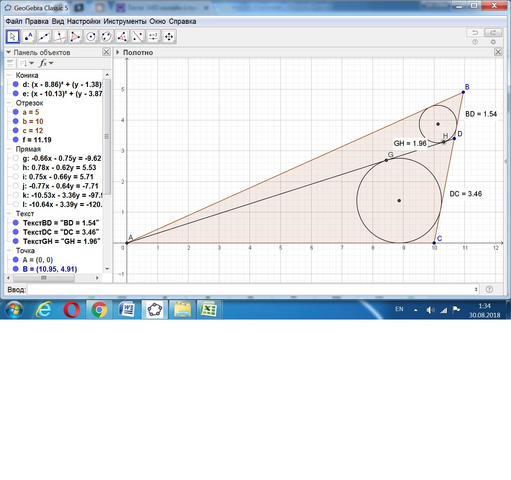
По заданию сторона АД разделена точкой Д на отрезки длиной (20/13) и (45/13).
Косинус угла В = (144 + 100 - 25)/(2*10*12) = 23/40.
Находим длину АД:
АД = √(144+(400/169)-2*12*(20/13)*(23/40)) = √125,1361 ≈ 11,18642.
Находим полупериметры и площади (по формуле Герона) треугольников АВД и АДС.
р(АВД) = 12,36244317,S
= 7,552186246
.
р(АДС) = 12,32398164, S
=16,99241669
.
Отсюда находим радиусы вписанных окружностей: r = S/p.
r(АВД) = 0.610898, r(АДС) = 1.378829.
Находим углы ВАД и ДАС:
∠ВАД = 6,46060914
°, ∠ДАС = 17,68623886°
.
Далее по формуле L = r/(tg(α/2)) находим длины касательных от точки А до точек касания окружностей r1 и r2.
L1 = 10.82398, L2 = 8.862443.
Разность их и равна искомой длине: ΔL= 1,961539.