X⁴+3x³+2x²+x+6=0
(x⁴+2x²+1)+(3x³+x+5)=0
(x²+1)²+ (3х³+х+1)=0
(x²+1)²>0
обозначим (x²+1)²=а>0
3х³+х+1+а=0
решим графически
3х³= -х-1-a,
a>0
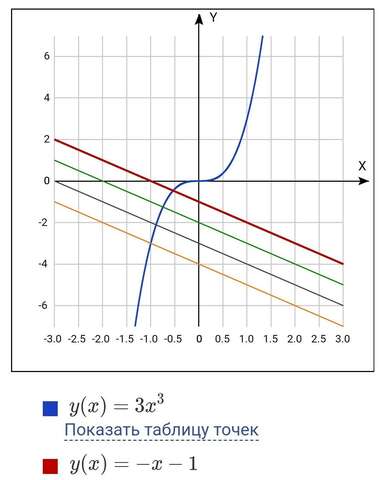
у=3х³ обозначено синим цветом
красным обозначено
у= х-1-a
при а=0
тонким зелёным при а=1
тонким черным при а =2
тонким оранжевым при а=3
Абсцисса точки пересечения графиков у=3х³ и у=-х-1-a и будет корнем уравнения.
как мы видим при любых а>0 она будет принимать только отрицательные значения,
соответственно корней положительных не будет у уравнения 3х³= -х-1-a, а следовательно, и у исходного
x⁴+3x³+2x²+x+6=0
что и требовалось доказать.