А мы пойдём другим способом:
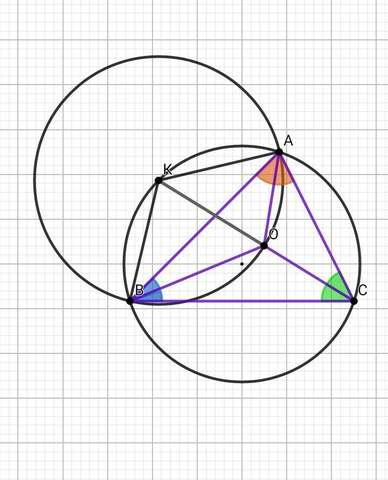
А) Рассмотрим рисунок 2 :
Пусть угол ВСО = а
Обозначим точку K, как точку пересечения прямой СО с окружностью, описанной около ∆ АВС, точка О – центр вписанной окружности ∆ АВС, тогда →
KB = KO = KA = 5 см - радиусы описанной окружности около треугольника АВО – по теореме о трилистнике или лемме о трезубце, или лемме Мансиона.
Рассмотрим ∆ ВКС:
По теореме синусов:
2R = BK / sin ВСО
2·5√2 = 5/ sina
sina = √2/4
cosC = cos2a = 1 – 2sin²a = 1 – 2·( √2/4 )² = 3/4 →
угол С = arccos( 3/4 )
Или можно поступить следующим образом:
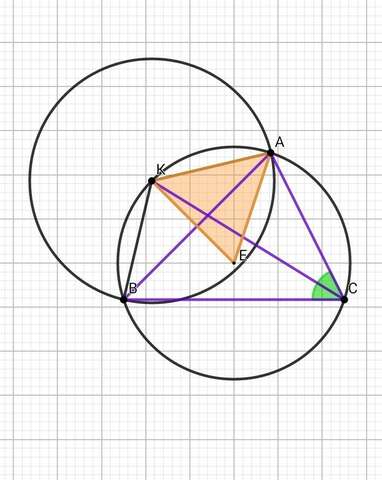
Б) Рассмотрим рисунок 1 :
точка Е - центр окружности, описанной около треугольника АВС
KE = AE = 5•( корень из 2 )
Рассмотрим тр. АКЕ:
По теореме косинусов:
АК^2 = АЕ^2 + КЕ^2 - 2• АЕ•КЕ•cos AEK
25 = 50 + 50 - 2•50•cos AEK
cos AEK = 3/4
угол АЕК = arccos( 3/4 )
Угол АСВ является вписанным углом окружности с центром в точке Е
▪Вписанный угол равен половине дуги, на которую этот угол опирается ▪
Угол АСВ = ( 1/2 ) • U AKB
U BK = U KA - равные хорды ВА и КА стягивают равные дуги
Угол АСВ = ( 1/2 ) • U AKB = U KA = U BK
Угол АКЕ является центральным углом окружности с центром в точке Е
▪ Центральный угол равен дуге, на которую этот угол опирается ▪
Угол АКЕ = U KA
Значит, угол АСВ = угол АКЕ = arccos( 3/4 )
Также если сделать замену:
r - радиус описанной окружности около треугольника АОВ
R - радиус описанной окружности около треугольника АВС , тогда
угол АСВ = arccos( ( 2R^2 - r^2 )/ 2R^2 )
ОТВЕТ: угол С = arccos( 3/4 )