В равнобедренном треугольнике авс (ав=вс) точка h ортоцентр. Высота АК=9 см, а отрезок...

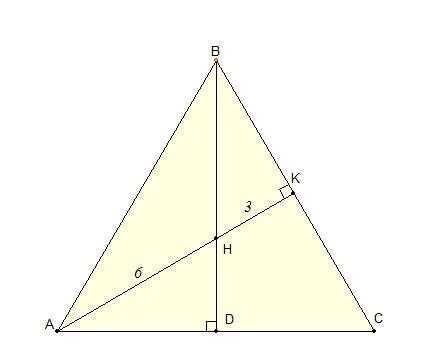
Поскольку HK=AK-AH=3 и AH:HK=2:1, то AK - медиана (и высота по условию). Тогда треугольник ABC - равносторонний и его площадь равна

$S=\frac{a^2\sqrt{3}}{4}$

где а - сторона. Найдем ее:

Поскольку треугольник равносторонний, то угол AHB = 120 градусов. Тогда по теореме косинусов:

$a^2=AB^2=AH^2+HB^2-2AH\cdot HB\cdot \cos\angle 120^\circ=\\ =81+81-2\cdot 81\cdot\left(-\frac{1}{2}\right)=243$

$S_{\triangle ABC}=\frac{243\sqrt{3}}{4}$