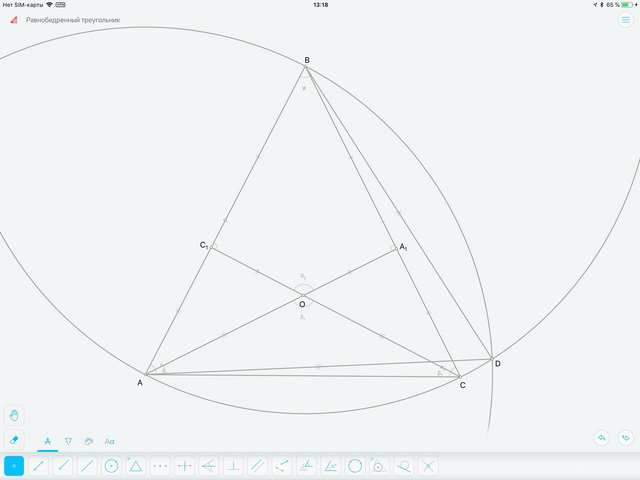
Две высоты равнобедренного ∆АВС АА₁ и СС₁ проведенные из вершин при основании, пересекаясь в точке О, образуют угол β₁= 126°.
1) Чему равен наименьший из углов АВС?
2) С помощью циркуля и линейки постройте угол на 6° больше чем наименьший угол ∆АВС.
1) Рассмотрим 4-угольник OCВА₁:
- ∠δ₁=∠δ₂=126°. (т.к. углы вертикальные),
- ∠С₁=∠А₁ (т.к. АА₁ и СС₁ - высоты),
- ∠γ=360°-90°*2-126°=54°.
∆АВС - равнобедренный, ∠γ₁=54°=>∠α₁=∠α₂=(180°-54°)/2=63°=>Наименьший ∠γ=54°.
2) ∠ε=54°+6°=60°. Чтобы получить этот угол при помощи линейки и циркуля нужно построить равносторонний треугольник (∆ABD) со стороной АВ.