| х²-x-1 | = 2x-1
Для начала исследуем
| х²-x-1 |
х²-x-1=0
ax²+bx+c=0
a= 1
b= -1
c= -1
D=b²-4ac=(-1)²-4•1•(-1)=5
x¹'²=(-b±✓D)/(2a)
x¹'²= ½(1±✓5)
при x²-x-1≥0, то есть при
х≥½(1+✓5) и х≤½(1-✓5)
| х²-x-1 |=х²-x-1
при x²-x-1<0, то есть при<br>½(1-✓5)<х<½(1+✓5)<br>| х²-x-1 |= -(х²-x-1)= -x²-x+1
и
| х²-x-1 |
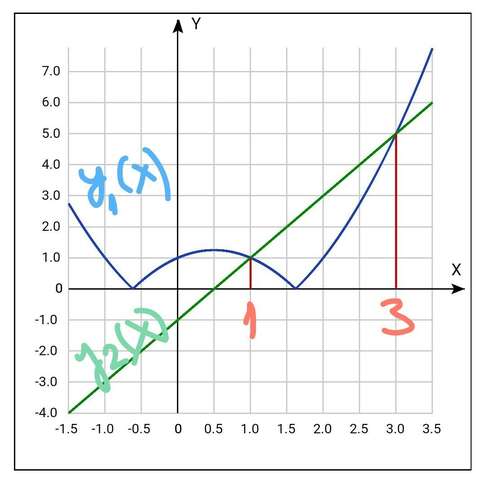
Теперь построим график:
у1(х)=| х²-x-1 | ( синий график)
у1(х)=х²-x-1, при
х≥½(1+✓5) и х≤½(1-✓5)
у1(х)=-x²-x+1 при
½(1-✓5)<х<½(1+✓5)<br>
и
у2(х)=2x-1 ( зелёный график )
точки для построения:
(х,у)¹=(0;-1)
(х,у)²=(½;0)
Точки пересечения графиков
у¹(х) и у²(х)
будут
(х,у)¹=(1;1)
(х,у)²=(3;5)
Поэтому наши решения будут
х¹=1
х²=3
Корни можно проверить непосредственной подстановкой в уравнение
| х²-x-1 | = 2x-1
х¹=1
|1²-1-1|=2•1-1
1=1 верно
х²=3
|3²-3-1|=2•3-1
5=5 верно
Ответ
х¹=1
х²=3