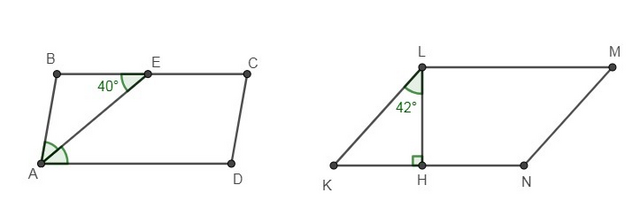
а) Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник ⇒ ∠ВАЕ = ∠ВЕА = 40°
∠А = 2∠ВАЕ = 2 * 40 = 80° (так как АЕ - биссектриса ∠А)
Сумма соседних углов параллелограмма равна 180° ⇒
∠В = 180 - ∠А = 180 - 80 = 100°
Противоположные углы параллелограмма равны ⇒
∠С = ∠А = 80°
∠D = ∠В = 100°
Ответ: 80°; 80°; 100°; 100°.
-------------------------------------------------------------------------
б) ΔKLH - прямоугольный ⇒ ∠К = 90 - 42 = 48°
Сумма соседних углов параллелограмма равна 180° ⇒
∠L = 180 - ∠K = 180 - 48 = 132°
Противоположные углы параллелограмма равны ⇒
∠M = ∠K = 48°
∠N = ∠L = 132°
Ответ: 48°; 48°; 132°; 132°.