Найдите область определения выражений:|x| > 4|x| <= 4|x| > -4Спасибо заранее

Question

Найдите область определения выражений:
|x| > 4
|x| <= 4<br>|x| > -4
Спасибо заранее

Comments

ООФ: любые действ. значения х. Проверь условие

---

оно именно такое

---

Это 9 класс

---

под знаком модуля может стоять любое число - это область определения. А вот , если решить неравенство, то тогда получим , какие на самом деле "х" будут.

---

Мне сказали найти область определения этих выражений через систему неравенств

Answer 1

4\; ,\\\\a)\; \; x\geq 0\; \; \Rightarrow \; \; |x|=x\; ,\; \; x>4\\\\b)\; \; x<0\; \; \Rightarrow \; \; |x|=-x\; ,\; \; -x>4\; \; \Rightarrow \; \; x<-4\\\\|x|>4\; \; \Rightarrow \; \; \left [ {{x>4} \atop {-x<-4}} \right. \; \; \Rightarrow \; \; \underline {x\in (-\infty,-4)\cup (4,+\infty )}\\\\2)\; \; |x|\leq 4\; ,\\\\a)\; \; x\geq 0\; \; \Rightarrow \; \; |x|=x\; ,\; \; x\leq 4\\\\b)\; \; x<0\; \; \Rightarrow \; \; |x|=-x\; ,\; \; -x\leq 4\; \; \Rightarrow \; \; x\geq -4" alt="|x|=\left \{ {{x\; ,\; esl\; \; x\geq 0} \atop {-x\; ,\; esli\; \; x<0}} \right. \\\\\\1)\; \; |x|>4\; ,\\\\a)\; \; x\geq 0\; \; \Rightarrow \; \; |x|=x\; ,\; \; x>4\\\\b)\; \; x<0\; \; \Rightarrow \; \; |x|=-x\; ,\; \; -x>4\; \; \Rightarrow \; \; x<-4\\\\|x|>4\; \; \Rightarrow \; \; \left [ {{x>4} \atop {-x<-4}} \right. \; \; \Rightarrow \; \; \underline {x\in (-\infty,-4)\cup (4,+\infty )}\\\\2)\; \; |x|\leq 4\; ,\\\\a)\; \; x\geq 0\; \; \Rightarrow \; \; |x|=x\; ,\; \; x\leq 4\\\\b)\; \; x<0\; \; \Rightarrow \; \; |x|=-x\; ,\; \; -x\leq 4\; \; \Rightarrow \; \; x\geq -4" align="absmiddle" class="latex-formula">

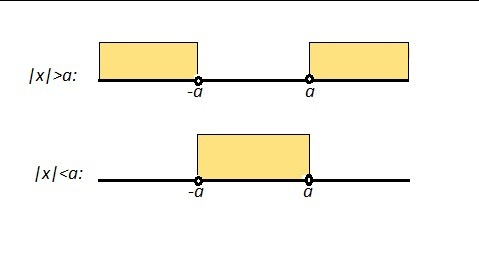
-4\; ,\\\\Tak\; kak\; \; |x|\geq 0\; ,\; to\; \; |x|>-4\; \; tem\; \; bolee\; \; pri\; \; \underline {x\in (-\infty ,+\infty )}.\\\\\\Pravilo:\; \; 1)\; \; |x|>a\; \; \Leftrightarrow \; \; \left [ {{x>a} \atop {x<-a}} \right. \; \; ili\; \; \; \underline {x\in (-\infty ,-a)\cup (a,+\infty )}\\\\2)\; \; |x|<a\; \; \Leftrightarrow \; \; -a<x<a\; \; \; ili\; \; \; \underline {x\in (-a,a)\; }." alt="|x|\leq 4\; \; \Rightarrow \; \; \left \{ {{x\leq 4} \atop {x\geq -4}} \right. \; \; \Rightarrow \; \; \underline {x\in [-4,4\, ]}\\\\3)\; \; |x|>-4\; ,\\\\Tak\; kak\; \; |x|\geq 0\; ,\; to\; \; |x|>-4\; \; tem\; \; bolee\; \; pri\; \; \underline {x\in (-\infty ,+\infty )}.\\\\\\Pravilo:\; \; 1)\; \; |x|>a\; \; \Leftrightarrow \; \; \left [ {{x>a} \atop {x<-a}} \right. \; \; ili\; \; \; \underline {x\in (-\infty ,-a)\cup (a,+\infty )}\\\\2)\; \; |x|<a\; \; \Leftrightarrow \; \; -a<x<a\; \; \; ili\; \; \; \underline {x\in (-a,a)\; }." align="absmiddle" class="latex-formula">

Смотри рисунок.

---