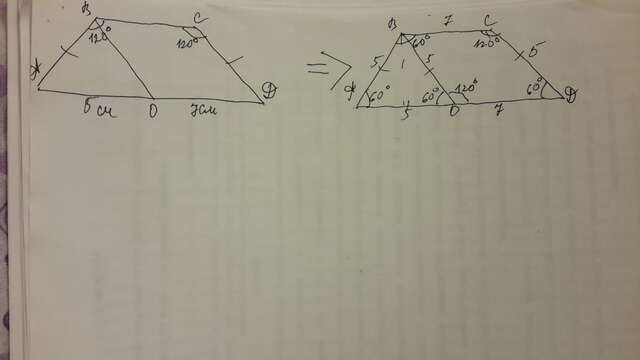
Думаю,что так: угол ВАД= СДА = 60 градусов,т.к.СД параллельна ВО ,а ВС параллельна АД ,то угол ВОД = 120 градусов и поэтому угол ОВС равен 60 градусов, угол АВО= АВС -ОВС= 120-60=60 ГРАДУСОВ, ТОГДА УГОЛ ВОА =180-(60+60)=60 градусов ,получается,что треугольник АВО равносторонний ,т.е. АВ=ВО=АО= 5 СМ , СД =АВ по условию,значит СД= 5 СМ, ВС=ОД =7 см т.к ОВСД- параллелограмм .
В итоге:АВ=СД=5 СМ, АД=АО+ОД=5+7=12 СМ, ВС=7 СМ,
Р=5+7+5+12=29СМ