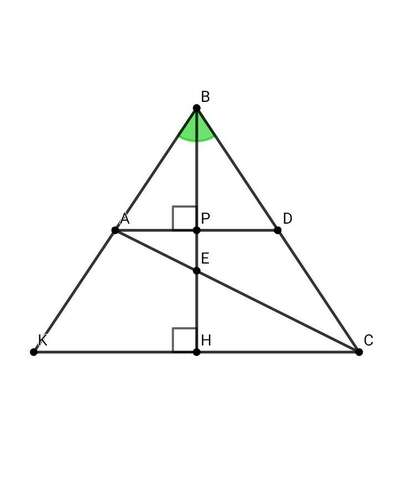
• Рассмотрим тр. АВD:
BP - биссектриса и высота
Значит, тр. ABD - равнобедренный , АB = BD , АР = PD = ( 1/2 ) • AD = ( 1/2 ) • 36 = 18
• Проведём из точки С прямую, параллельную прямой AD до пересечения с прямой АВ в точке К.
• Отсюда BD = DC = AB = AK =>
тр. ВСK - равнобедренный , ВК = ВС ,
ВР перпендикулярен АD
Соответственно, ВН перпендикулярен КС
ВН - биссектриса, медиана , высота.
• Медианы ВН и АС тр. ВСК пересекаются в точке Е =>
Медианы треугольника пересекаются в одной точке и точкой пересечения делятся в отношении 2 : 1 , считая от вершины
• ВЕ : ЕН = 2 : 1
Отрезок ВН состоит 3 равных частей, 2 из которых состоит отрезок ВЕ и 1 такая же часть - отрезок ЕН.
• Возьмём одну часть за Х , тогда ВЕ = 2х , ЕН = х
ВЕ = 2•х = 36
х = 18
Значит, ЕН = 18 , ВЕ = 36 , ВН = ВЕ + ЕН = 36 + 18 = 54
Но ВР = РН = ( 1/2 ) • ВН = ( 1/2 ) • 54 = 27
РЕ = ВЕ - ВР = 36 - 27 = 9
• Рассмотрим тр. АВР (угол АРВ = 90°):
По теореме Пифагора:
АВ^2 = АР^2 + ВР^2
АВ^2 = 18^2 + 27^2 = 9^2 • ( 2^2 + 3^2 ) =
81 • 13
АВ = 9\/13
Соответственно, ВС = 2•АВ = 2 • 9\/13 = 18\/13
• Рассмотрим тр. АРЕ (угол АРЕ = 90°):
По теореме Пифагора:
АЕ^2 = АР^2 + РЕ^2
АЕ^2 = 18^2 + 9^2 = 9^2 • ( 2^2 + 1 ) = 81 • 5
АЕ = 9\/5
• По свойству медианы:
ЕС = 2 • АЕ = 2 • 9\/5 = 18\/5
АС = АЕ + ЕС = 9\/5 + 18\/5 = 27\/5
ОТВЕТ: 9\/13 , 27\/5 , 18\/13 .