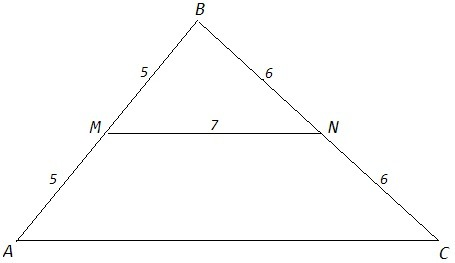
AC - основание треугольника, MN - средняя линия.
Средняя линия соединяет середины двух сторон, параллельна третьей стороне и равна ее половине.
AM=MB=5, BN=NC=6, MN||AC, MN=AC/2=7
AB=AM+MB=5*2=10
BC=BN+NC=6*2=12
AC=2MN=7*2=14
P(ABC)=AB+BC+AC=10+12+14=36
Или:
P(MBN)=5+6+7=18
Параллельные отсекаю от угла подобные треугольники,
△ABC~△MBN, k=AC/MN=2
Периметры подобных треугольников относятся как коэффициент подобия,
P(ABC)=2P(MBN)=18*2=36