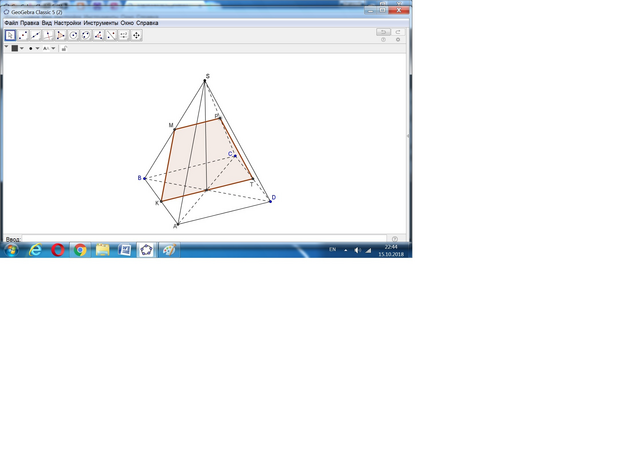
Сечением является равнобокая трапеция с нижним основанием, равным стороне основания, верхнее равно половине стороны основания.
Находим высоту пирамиды Н:
Н = (а/2)*tg60° = 2*√3 см.
Боковая сторона трапеции равна половине бокового ребра L.
Проекция бокового ребра на основание равна половине диагонали основания.
L = √(H² + (d/2)²) = √(12 + (2√2)²) = √(12 + 8) = √20 = 2√5 см.
Боковые стороны КМ и РТ равны 2√5/2 = √5 см.
Находим высоту h сечения:
h = √(√5)² - ((4-2)/2)²) = √(5 - 1) = √4 = 2 см.
Получаем площадь сечения S = ((4 + 2)/2)*2 = 6 см².