3)
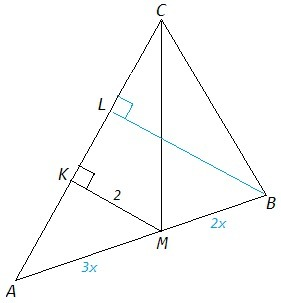
AC=3/2 BC
Площади треугольников с равным углом относятся как произведения сторон, составляющих угол (по формуле площади через две стороны и угол между ними).
S(MCA)/S(MCB)= AC*MC/BC*MC =AC/BC =3/2
По теореме косинусов:
AB^2= AC^2 +BC^2 -2AC*BC*cos60 =
9/4 BC^2 +BC^2 -3/2 BC^2 =7/4 BC^2 <=> AB= BC√7/2
По теореме о биссектрисе:
AM/BM=AC/BC =3/2
BL⊥AC: △ABL~△AMK, k=AB/AM =5/3
BL=MK*k =10/3
△BCL - прямоугольный с углом 60:
BC= BL*2√3/3 =20√3/9
AB=BC√7/2 =10√21/9
5)
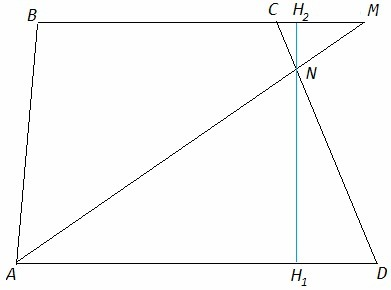
AD=a, BC=b, CM=x, H1H2=h
△AND~△MNC
NH1/NH2 =a/x
NH1= h*a/(a+x)
S(ABCD)/2 =S(AND) <=>
(a+b)h/4 = a^2*h/2(a+x) <=>
(a+b)/2 = a^2/(a+x) <=>
x= 2a^2/(a+b) -a =a(a-b)/(a+b) =12*4/20=2,4