1. В равнобедренной трапеции высота делит большее основание ** отрезки, равные 6 и...

Question

1. В равнобедренной трапеции высота делит большее основание на отрезки, равные 6 и 13см.Найдите среднюю линию трапеции 2. В трапеции mhkp угол m 90 градусов, угол k 150 градусов, hk 3 см, диагональ мк перпендикулярна боковой стороне kp. Найдите среднюю линию трапеции

Answer 1

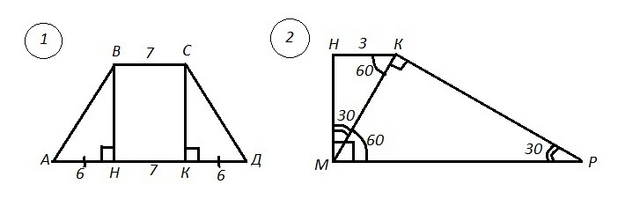
1)  АВСД - трапеция, АВ-СД, ВН⊥АД , АН=6 см , НД=13 см.

Проведём СК⊥АД, тогда АН=КД=6 см , НК=13-6=7 см , НК=ВС=7 см, АД=АН+НД=6+13=19 см.

Средняя линия трапеции = (АД+ВС)/2=(7=19+7)/2=26/2=13 см.

Замечание . Средняя линия трапеции и отрезок НД всегда равны, если трапеция равнобедренная.

2)  МНКР - трапеция, ∠М=90°  ,  ∠К=150°  ,  НК=3 см ,  МК⊥КР.

∠МКН=∠НКР-∠СКР=150°-90°=60°  ⇒  в ΔМКН  ∠КМН=90°-∠МКР=90°-60°=30°  ⇒  катет КН, лежащий против угла в 30° равен половине гипотенузы  ⇒  гипотенуза МК=2*КН=2*3=6 см.

Рассм. ΔМКР , ∠МКР=90° , ∠КМР=∠М-∠КМН=90°-30°=60°  ⇒  ∠МРК=30°.

Против угла в 30° лежит катет МК, равный половине гипотенузы МР  ⇒   МР=2*МК=2*6=12 см

Средняя линия трапеции = (МР+КН)/2=(12+3)/2=15/2=7,5 см.

---