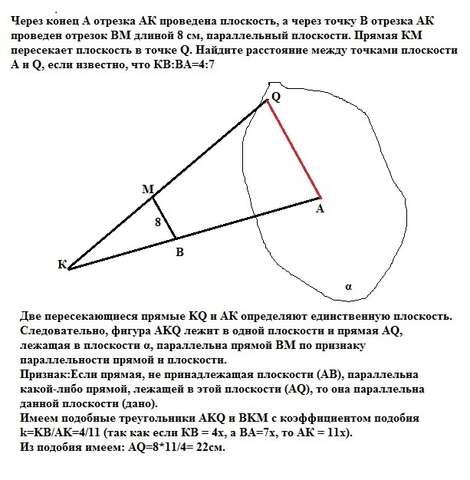
Две пересекающиеся прямые KQ и АК определяют единственную плоскость. Следовательно, фигура AKQ лежит в одной плоскости и прямая AQ, лежащая в плоскости α, параллельна прямой ВМ по признаку параллельности прямой и плоскости.
Признак:Если прямая, не принадлежащая плоскости (AB), параллельна какой-либо прямой, лежащей в этой плоскости (AQ), то она параллельна данной плоскости (дано).
Имеем подобные треугольники AKQ и BKM с коэффициентом подобия k=KB/AK=4/11 (так как если КВ = 4х, а ВА=7х, то АК = 11х).
Из подобия имеем: AQ=8*11/4= 22см. Это ответ.