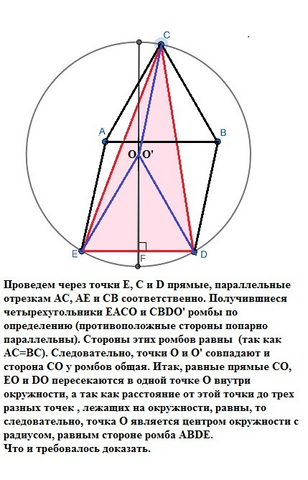
Проведем через точки Е, С и D прямые, параллельные отрезкам АС, АЕ и СВ соответственно. Получившиеся четырехугольники ЕАСО и СВDО' ромбы по определению (противоположные стороны попарно параллельны). Стороны этих ромбов равны (так как АС=ВС). Следовательно, точки О и О' совпадают и сторона СО у ромбов общая. Итак, равные прямые СО, ЕО и DO пересекаются в одной точке О внутри окружности, а так как расстояние от этой точки до трех разных точек , лежащих на окружности, равны, то следовательно, точка О является центром окружности с радиусом, равным стороне ромба ABDE. Что и требовалось доказать.