100 баллов BD – диагональ параллелограмма ABCD. Найдите величину ∠BAD, если ∠BAD+∠ADB=80∘...

Question

100 баллов BD – диагональ параллелограмма ABCD. Найдите величину ∠BAD, если ∠BAD+∠ADB=80∘ и ∠BCD+∠ABD=140∘.

Answer 1

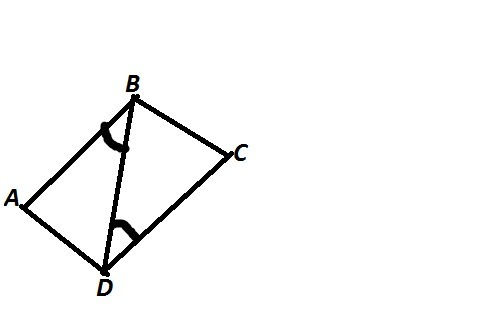
1)∠BAD+∠ADB=80∘ ⇒ ∠ ABD = 180° - (∠BAD+∠ADB) = 180° - 80° = 100°

2)∠BAD = ∠BDC = 100° (так как накрест лежащие)

3)∠BCD+∠ABD=140∘ }

                                   } ⇒ ∠BCD + ∠ABD = ∠BAD +∠ABD = 140∘ ⇒

∠BAD = ∠BDC = 100°}

⇒∠DBC = 180° - (∠BAD +∠ABD) = 180° - 140° = 40°

4)∠DBC = ∠ADB = 40° (так как накрест лежащий)

5)∠BAD = 180° - (∠ABD + ∠ADB) = 180° - (40° + 100°) = 180° - 140° = 40°

---

Comments

1) BAD+ADB=80 => ABD=180-(BAD+ADB)=1002) BCD+ABD=140 <=> BCD=140-ABD=40 =BAD

Answer 2

∠ABD=180°-(∠BAD+∠ADB)=180°-80°=100° (сумма углов треугольника 180°)

∠BCD+∠ABD=140° <=> ∠BCD=140°-∠ABD=140°-100°=40°

∠BAD=∠BCD=40° (противоположные углы параллелограмма равны)

---