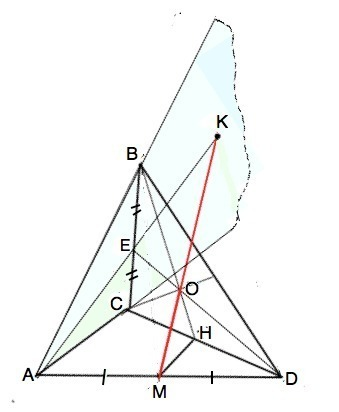
По свойству медиан точка их пересечения О делит их в отношении 2:1, считая от вершины (свойство).
Медиана из D пересекает ВС в т.Е. ВЕ=СЕ, ⇒ АЕ медиана ∆ АВС.
МО лежит в плоскости АЕD, которая пересекается с плоскостью АВС по прямой АЕ.
В ∆ АЕD точка М - середина АD, АМ=DМ, ЕО=0,5 DО, следовательно, прямые АЕ и МО не параллельны и пересекутся вне плоскости ∆ ВСD в некоторой точке К, принадлежащей плоскости АВС и лежащей на продолжении медины АЕ.