2\; \; \; \; .\end{array}\right\\\\1)\; \; \int\limits^{+\infty }_{-\infty }\, f(x)\, dx=1\; \; \to \; \; \int\limits_{-\infty }^{0}\, f(x)\, dx+\int\limits^2_0\, f(x)\, dx+\int\limits^{+\infty }_2\, f(x)\, dx=\\\\=\int\limits^2_0\, cx\, dx=c\cdot \frac{x^2}{2}\, \Big | _0^2=\frac{c}{2}\cdot (4-0)=2c=1\; ,\; \; \boxed {c=\frac{1}{2}}\\\\2)\; \; M(X)=\int\limits^{+\infty }_{-\infty}f(x)\, dx" alt="f(x)=\left\{\begin{array}{ccc}0,\; esli\; x\leq 0\; ,\; \; \; \; \; \\c\cdot x\; ,\; esli\; 02\; \; \; \; .\end{array}\right\\\\1)\; \; \int\limits^{+\infty }_{-\infty }\, f(x)\, dx=1\; \; \to \; \; \int\limits_{-\infty }^{0}\, f(x)\, dx+\int\limits^2_0\, f(x)\, dx+\int\limits^{+\infty }_2\, f(x)\, dx=\\\\=\int\limits^2_0\, cx\, dx=c\cdot \frac{x^2}{2}\, \Big | _0^2=\frac{c}{2}\cdot (4-0)=2c=1\; ,\; \; \boxed {c=\frac{1}{2}}\\\\2)\; \; M(X)=\int\limits^{+\infty }_{-\infty}f(x)\, dx" align="absmiddle" class="latex-formula">
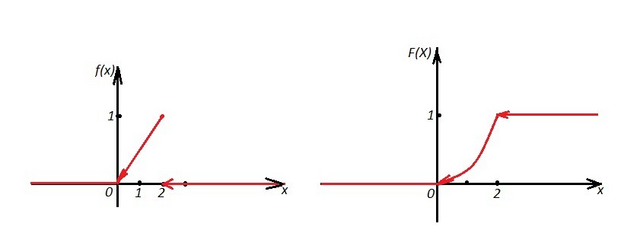
![3)\; \; F(X)=\int\limits^{x}_{-\infty }\, f(t)\, dt\\\\x\in (-\infty ,0\, ]:\; \; F(X)=\int\limits^{x}_{-\infty}\, 0\cdot dt=0\; ,\\\\x\in (0,2\, ]:\; \; F(x)=\int \limits _{-\infty }^0\, 0\cdot dt+\int\limits^{x}_0\, \frac{1}{2}\cdot t\, dt=\frac{1}{2}\cdot \frac{t^2}{2}\, \Big |_0^{x}=\frac{1}{4}\cdot (x^2-0)=\frac{x^2}{4}\; ,\\\\x\in (2,+\infty ):\; \; F(X)=\int\limits_{-\infty }^0\, 0\cdot dt+\int \limits _0^2\, \frac{1}{2}\cdot t\, dt+\int\limits_{2}^{x}\, 0\cdot dt=1](https://tex.z-dn.net/?f=3%29%5C%3B%20%5C%3B%20F%28X%29%3D%5Cint%5Climits%5E%7Bx%7D_%7B-%5Cinfty%20%7D%5C%2C%20f%28t%29%5C%2C%20dt%5C%5C%5C%5Cx%5Cin%20%28-%5Cinfty%20%2C0%5C%2C%20%5D%3A%5C%3B%20%5C%3B%20F%28X%29%3D%5Cint%5Climits%5E%7Bx%7D_%7B-%5Cinfty%7D%5C%2C%200%5Ccdot%20dt%3D0%5C%3B%20%2C%5C%5C%5C%5Cx%5Cin%20%280%2C2%5C%2C%20%5D%3A%5C%3B%20%5C%3B%20F%28x%29%3D%5Cint%20%5Climits%20_%7B-%5Cinfty%20%7D%5E0%5C%2C%200%5Ccdot%20dt%2B%5Cint%5Climits%5E%7Bx%7D_0%5C%2C%20%5Cfrac%7B1%7D%7B2%7D%5Ccdot%20t%5C%2C%20dt%3D%5Cfrac%7B1%7D%7B2%7D%5Ccdot%20%5Cfrac%7Bt%5E2%7D%7B2%7D%5C%2C%20%5CBig%20%7C_0%5E%7Bx%7D%3D%5Cfrac%7B1%7D%7B4%7D%5Ccdot%20%28x%5E2-0%29%3D%5Cfrac%7Bx%5E2%7D%7B4%7D%5C%3B%20%2C%5C%5C%5C%5Cx%5Cin%20%282%2C%2B%5Cinfty%20%29%3A%5C%3B%20%5C%3B%20F%28X%29%3D%5Cint%5Climits_%7B-%5Cinfty%20%7D%5E0%5C%2C%200%5Ccdot%20dt%2B%5Cint%20%5Climits%20_0%5E2%5C%2C%20%5Cfrac%7B1%7D%7B2%7D%5Ccdot%20t%5C%2C%20dt%2B%5Cint%5Climits_%7B2%7D%5E%7Bx%7D%5C%2C%200%5Ccdot%20dt%3D1 "3)\; \; F(X)=\int\limits^{x}_{-\infty }\, f(t)\, dt\\\\x\in (-\infty ,0\, ]:\; \; F(X)=\int\limits^{x}_{-\infty}\, 0\cdot dt=0\; ,\\\\x\in (0,2\, ]:\; \; F(x)=\int \limits _{-\infty }^0\, 0\cdot dt+\int\limits^{x}_0\, \frac{1}{2}\cdot t\, dt=\frac{1}{2}\cdot \frac{t^2}{2}\, \Big |_0^{x}=\frac{1}{4}\cdot (x^2-0)=\frac{x^2}{4}\; ,\\\\x\in (2,+\infty ):\; \; F(X)=\int\limits_{-\infty }^0\, 0\cdot dt+\int \limits _0^2\, \frac{1}{2}\cdot t\, dt+\int\limits_{2}^{x}\, 0\cdot dt=1")
2\; .\; \; \; \; \end{array}\right" alt="F(X)=\left\{\begin{array}{ccc}0\; ,\; esli\; x\leq 0\; ,\; \; \; \\\frac{x^2}{4}\; ,\; esli\; 02\; .\; \; \; \; \end{array}\right" align="absmiddle" class="latex-formula">
