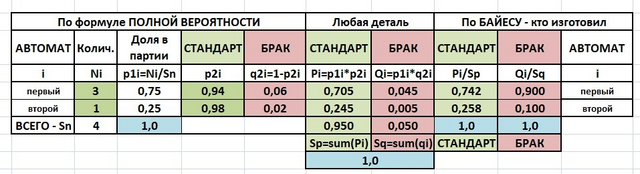
Решение задачи на рисунке в приложении.
В таблице заполнено решение по формуле полной вероятности и формуле Байеса и, поэтому, можно ответить на вопросы не только данной задачи.
РЕШЕНИЕ
Задача состоит из двух событий:
Р1 - взять любую деталь из партии. Эта вероятность зависит от количества деталей в партии. n1 = 3x n2 = 1x
Всего деталей - n = 4x, P11 = 3/4 = 0.75, P12 = 1/4 = 0.25.
Проверяем по формуле полной вероятности: Р1 = 0,75+0,25 = 1 - всё правильно - других вариантов нет. (Не берем "чужие" детали)
Далее - вероятность брака - дана. q21 = 0.06, q22 = 0.002
Вероятность стандарта (не брак) находим по формуле: p21 = 1 - 21 = 0.94, p22 = 0.98
ЗАПОМИНАЕМ на всю жизнь.
Вероятность событий "И" - равна произведению вероятностей каждого. Вероятность событий "ИЛИ" - равна сумме вероятностей каждого.
Возвращаемся к задаче. Наше событие - И любая И брак ИЛИ с первого ИЛИ со второго автомата. В задаче ЛЮБАЯ деталь оказалась БРАК.
Sq = p11*q21 + p21*q22 = 0.045 + 0.005 = 0.05 - вероятность "любая брак". - И это ответ на вопрос а) р = 0,05 - ОТВЕТ
Не поленимся и находим решение - ЛЮБАЯ СТАНДАРТ (для понятий)
Sp = 0.705 + 0.245 = 0.95 - вероятность "любая стандарт".
Проверяем по формуле полной вероятности и получаем:
P(A) = Sp + Sq = 0.95 + 0.05 = 1 - всё правильно.
Переходим к вопросу б) - кто же изготовил эту бракованную деталь. Это уже - формула Байеса. Возвращаемся к столбику ЛЮБАЯ БРАК.
Из всех бракованных деталей Q1 = 0,045 делает первый, а Q2 = 0.005 - второй автомат. Находим долю брака у первого автомата
Q1/Sq = 0.045 / 0.05 = 0.9 - случайный брак первого автомата - ОТВЕТ
Случайныё брак второго автомата всего 0,1. Проверяем по формуле полной вероятности: Р(брак) = 0.9+0.1 = 1 - других бракоделов нет.
Здесь же видим, что вероятность любой и стандартной детали для первого автомата равна 0,742, а для второго - 0,258.
Вот такое универсальное решение для множества задач состоящих из двух событий.