Исследовать функцию y=(x-5)/e^(2x) и схематично построить её график.

$y(x) = \frac{x - 5}{ {e}^{2x} } = (x - 5) \cdot {e}^{ - 2x}$
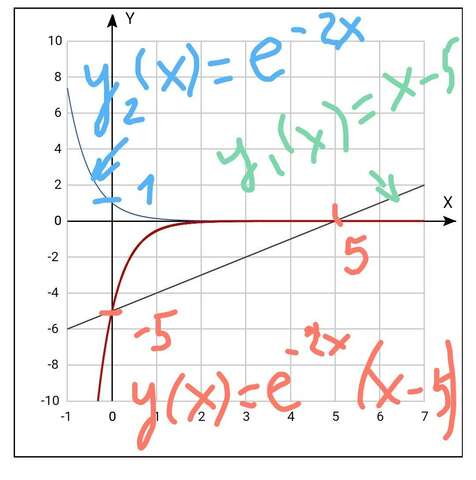
наша
функция( красный график)
получается как произведение функций
$y1(x) = (x - 5) \\ y2(x) = {e}^{ - 2x}$

1) область определения
$D_{y(x)}=x∈R$
2)область значений
$E_{y(x)}=y∈(-∞;0]$
3)нули функции

\\ = > (x - 5) \cdot {e}^{ - 2x} = 0 \\ = > x = 5" alt="y(x) = 0 = > \\ = > (x - 5) \cdot {e}^{ - 2x} = 0 \\ = > x = 5" align="absmiddle" class="latex-formula">
функция положительна
при х>5

4)x=0
$y(0) = (0 - 5) \cdot {e}^{ - 2 \cdot 0} = - 5$
5)
$y'(x)=((x - 5) \cdot {e}^{ - 2x} )'= \\ = (x - 5) \cdot( {e}^{ - 2x} )' + \\ + (x - 5 )' \cdot {e}^{ - 2x} = \\ = - 2(x - 5) {e}^{ - 2x} + 1 \cdot {e}^{ - 2x} = \\ = (- 2x - 9){e}^{ - 2x}$

6)
$y( - x) = \frac{ - x - 5}{ {e}^{ - 2x} }≠±y(x) \\$
функция общего вида,
не является чётной/нечётной

7) функция не является периодической
8) функция возрастающая