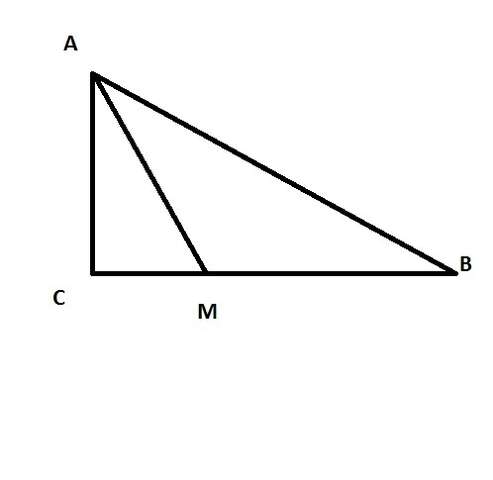
Найдем углы. Меньший х, следующий х+d , больший х+2d.
Уравнения: х+2d=90 и х+х+d+x+2d=180. x=30, d=30. углы 30, 60 и 90.
Если радиус описанной окружности равен 10, то гипотенуза равна 20.
Сторона АС лежит против угла в 30 градусов, она равна 20/2=10. СВ=10√3.
По свойству биссектрисы СМ:МВ=АС:АВ.
СМ: (10√3-СМ)=10:20⇒2*СМ=10√3-СМ.
СМ=10√3/3. АМ ищем по теореме Пифагора АМ=√(АС²+СМ²)=√100+300/9)=√(400/3) = 20/√3.